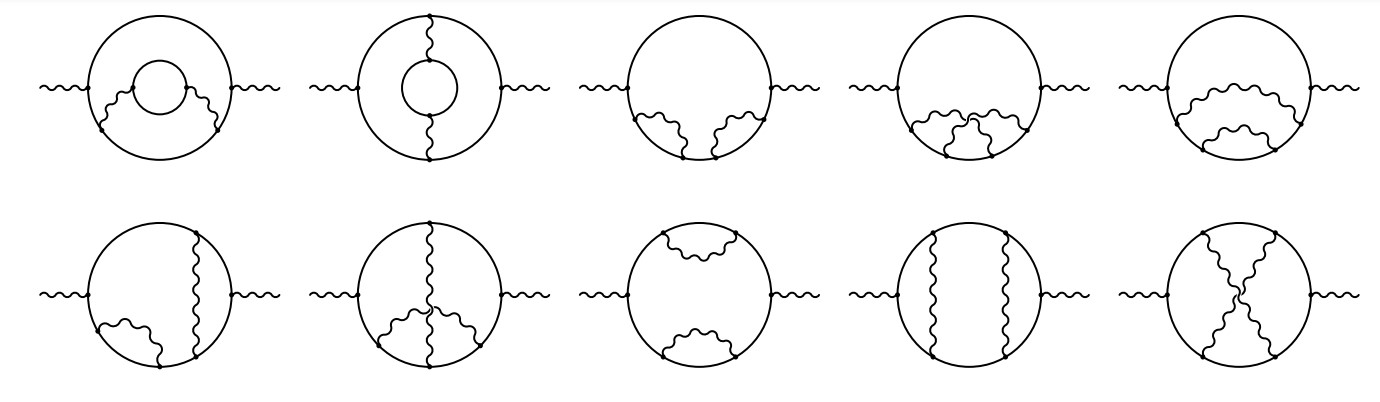
We calculate three-loop photon spectral density in QED with N different species of electrons. The obtained results were expressed in terms of iterated integrals, which can be either reduced to Goncharov’s polylogarithms or written in terms of one-fold integrals of harmonic polylogarithms and complete elliptic integrals. In addition, we provide threshold and high-energy asymptotics of the calculated spectral density. It is shown that the use of the obtained spectral density correctly reproduces separately calculated moments of corresponding photon polarization operator.
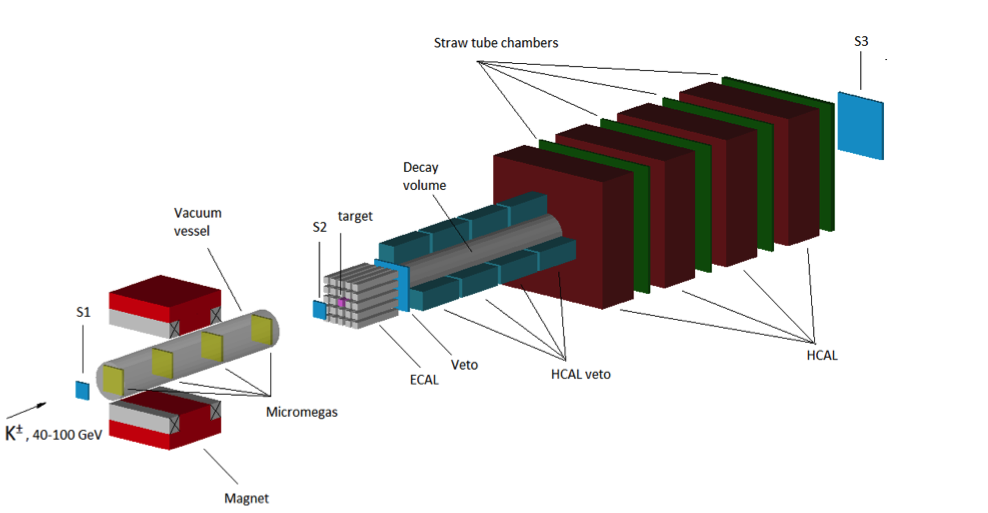
The decays KS,L → invisible have never been experimentally tested. In the Standard Model (SM), their branching ratios for the decay into two neutrinos are predicted to be extremely small, Br (KS,L → νν̄) ≲ 10−16. We consider several natural extensions of the SM, such as two-Higgs-doublet (2HDM), 2HDM and light scalar, and dark mirror sector models, that allow one to enhance the Br (KS,L → invisible) up to a measurable level. We briefly discuss the possible search for KS,L → invisible decays and KS,L oscillations into the dark sector at the NA64 experiment at CERN with the sensitivity to Br (KS,L → invisible) ≲ 10−7−10−5.
This introductory review is devoted to the newest section of the theory of symmetries -- the theory of quantum groups.
The principles of the theory of quantum groups are reviewed from the point of view of the possibility of their use for deformations of symmetries in physics models. The R-matrix approach to the theory of quantum groups is discussed in detail and is taken as the basis of the quantization of classical Lie groups, as well as some Lie supergroups. We start by laying out the foundations of non-commutative and non-cocommutative Hopf algebras. Much attention has been paid to Hecke and Birman-Murakami-Wenzl (BMW) R-matrices and related quantum matrix algebras. Noncommutative differential geometry on quantum groups of special types is discussed. Trigonometric solutions of the Yang-Baxter equations associated with the quantum groups GLq(N), SOq(N), Spq(2n) and supergroups GLq(N|M), Ospq(N|2m), as well as their rational (Yangian) limits, are presented. Rational R-matrices for exceptional Lie algebras and elliptic solutions of the Yang-Baxter equation are also considered. The basic concepts of the group algebra of the braid group and its finite dimensional quotients (such as Hecke and BMW algebras) are outlined. A sketch of the representation theories of the Hecke and BMW algebras is given, including methods for finding idempotents (quantum Young projectors) and their quantum dimensions. Applications of the theory of quantum groups and Yang-Baxter equations in various areas of theoretical physics are briefly discussed.
This is a modified version of the review paper published in 2004 as a preprint of the Max-Planck-Institut für Mathematik in Bonn.
We give a brief overview of the BRST approach to the gauge-invariant Lagrangian formulation for free massive higher-spin bosonic fields, focusing on two specific aspects. First, the theory is considered in four-dimensional flat space in terms of spin-tensor fields with two-component undotted and dotted indices. This leads to a significant simplification of the whole approach in comparison with the one where the fields with vector indices were used, since now there is no need to introduce a constraint responsible for the traces of the fields into the BRST charge. Second, we develop an extremely simple and clear procedure to eliminate all the auxiliary fields and prove that the BRST equations of motion identically reproduce the basic conditions for irreducible representations of the Poincáre group with a given mass and spin. Similar to the massless theory, the final Lagrangian for massive higher-spin fields is formulated in triplet form. The BRST formulation leads to a system of fields that are clearly subdivided into the basic spin s field, Zinoviev-like auxiliary fields, Singh–Hagen-like auxiliary fields, and special BRST auxiliary fields. The auxiliary fields can be partially eliminated by gauge fixing and/or using the equations of motion. This allows one to obtain formally different (with different numbers of auxiliary fields) but equivalent Lagrangian formulations.
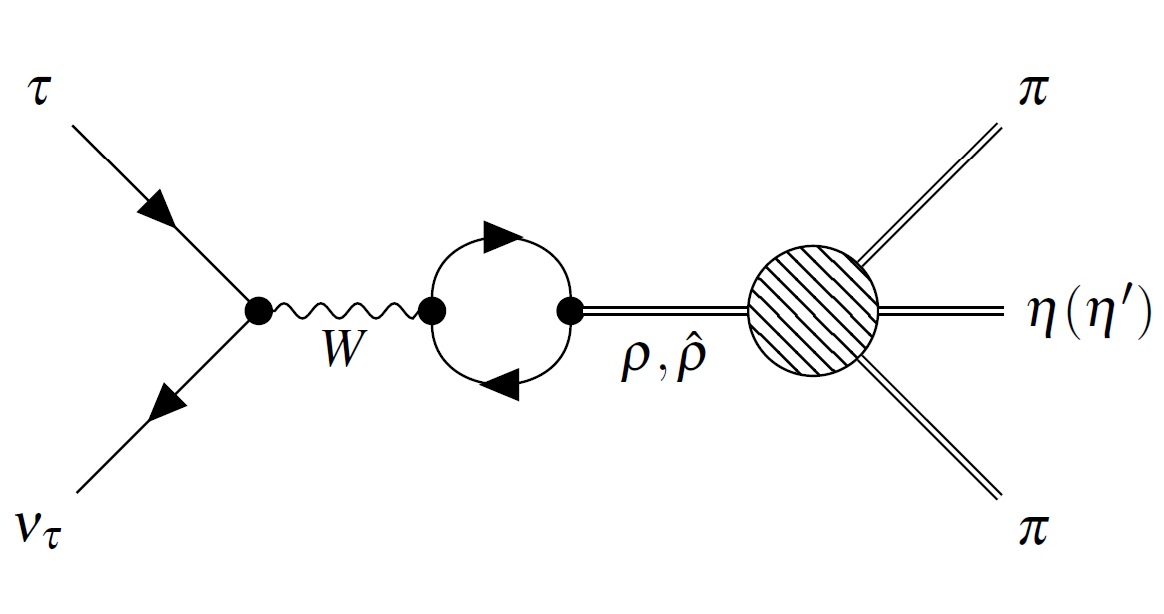
In the framework of the extended Nambu–Jona-Lasinio model, the processes τ → ππη(η′)ντ and τ → πηη(η′)ντ are considered taking into account mesons in the ground and first radially excited intermediate states. It is shown that in the processes τ → ππη(η′)ντ the vector channel is dominant, and in the processes τ → πηη(η′)ντ the main contribution is given by the axial-vector channel. The scalar meson a0 plays a dominant role in processes with two η mesons in the final state. The significance of the relative phase between the ground and first radially excited states for these processes is shown. The obtained results for the τ → ππηντ process are in satisfactory agreement with the recent experimental data from BaBar and CMD-3, which differ from the averaged values given in the PDG tables.
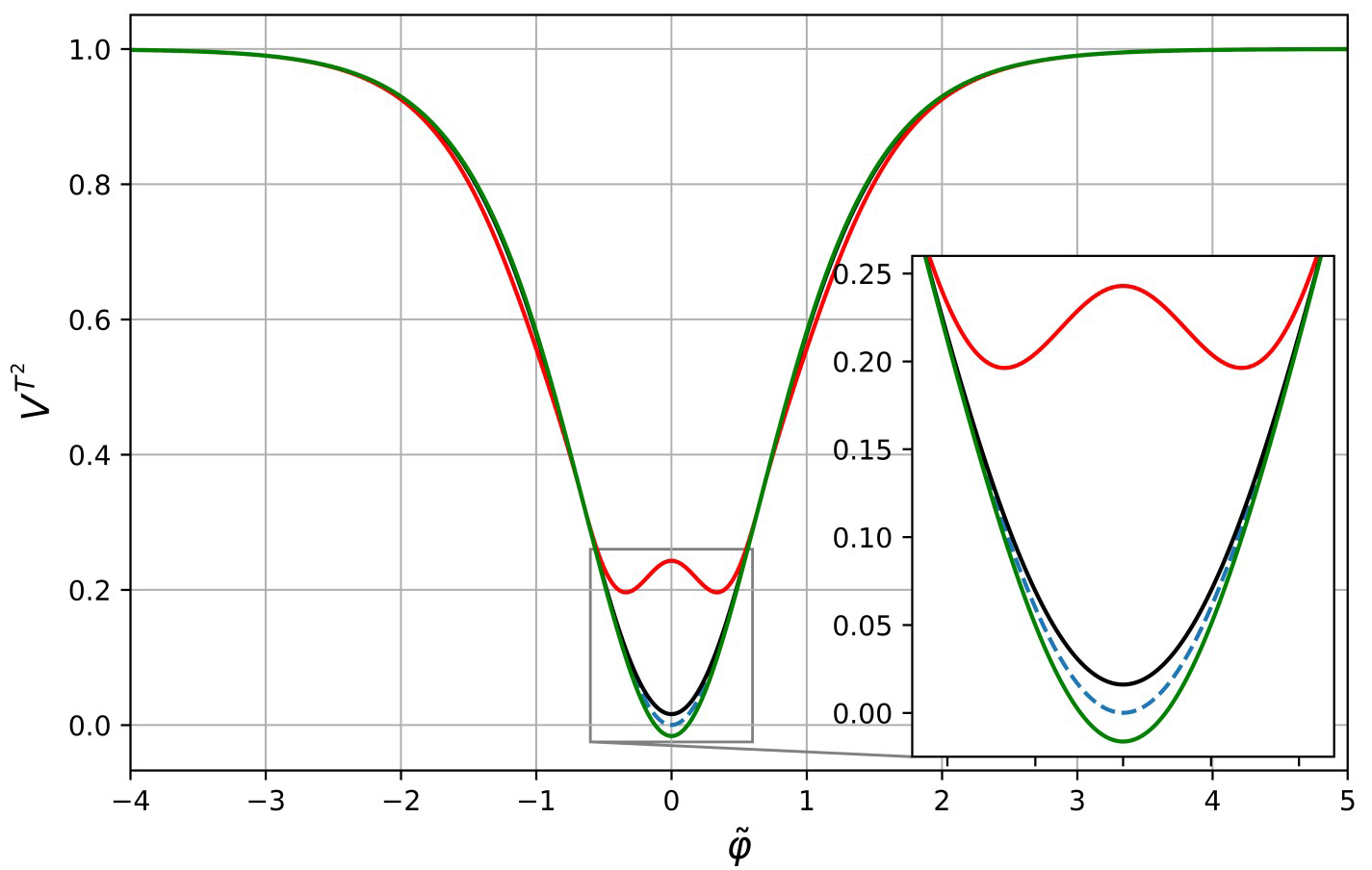
Using the generalized renormalisation group formalism, we calculate quantum corrections to the effective potential in α-attractor models describing the inflationary stage of the Universe evolution. We demonstrate that quantum corrections lead to a change in the initial classical potential, changing its value at the minimum, which can be interpreted as a manifestation of the cosmological constant or dark energy.