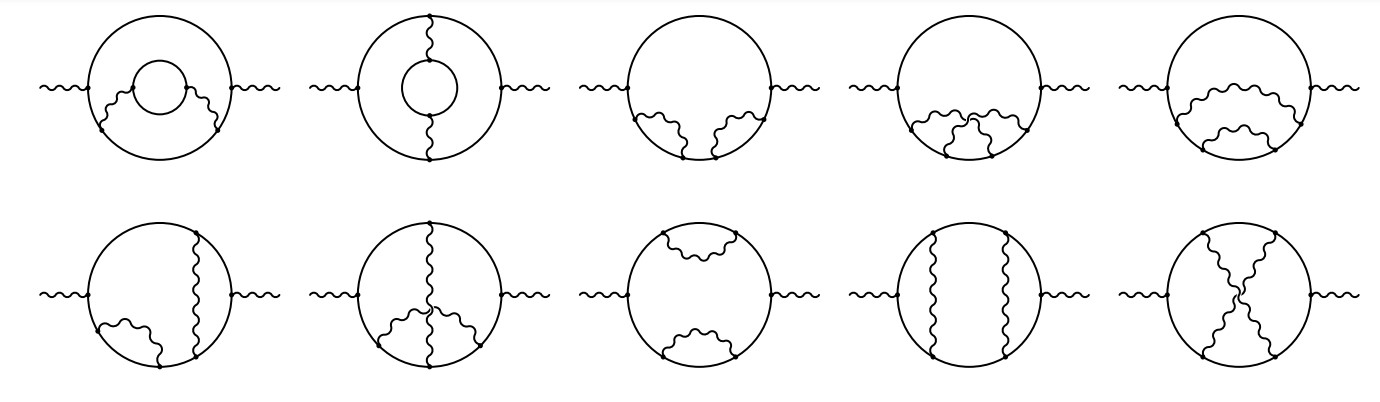
Мы вычисляем трехпетлевую спектральную плотность фотона в квантовой электродинамике с N различными видами электронов. Полученные результаты были выражены в виде повторных интегралов, которые могут быть либо сведены к полилогарифмам Гончарова, либо записаны в виде однократных интегралов от произведения гармонических полилогарифмов и полных эллиптических интегралов. Также мы приводим пороговую и высокоэнергетическую асимптотику рассчитанной спектральной плотности. Показано, что использование полученной спектральной плотности правильно воспроизводит отдельно вычисленные моменты соответствующего поляризационного оператора фотона.
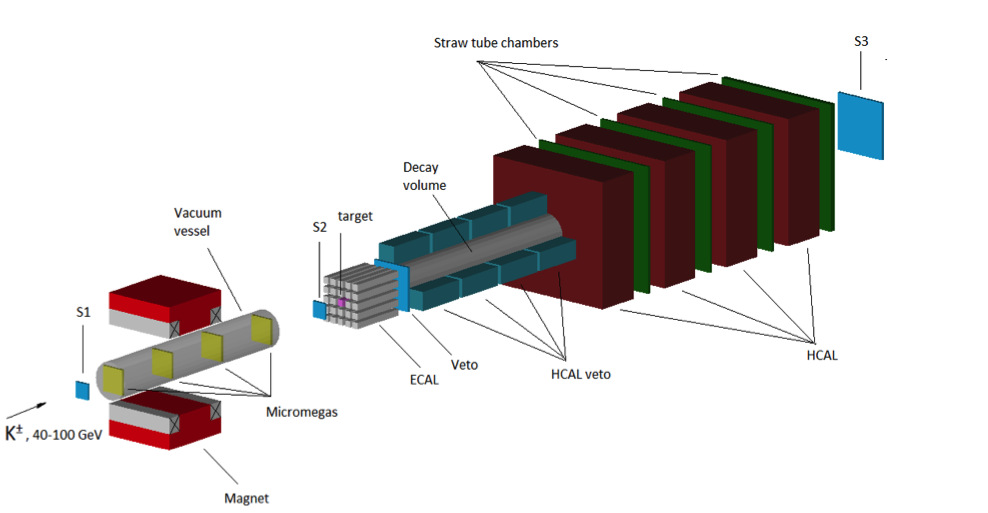
Распады KS,L → invisible никогда не проверялись экспериментально. В Стандартной Модели (СМ) их коэффициенты ветвления для распада на два нейтрино предсказываются как чрезвычайно малые: Br (KS,L → νν̄) ≲ 10−16. Мы рассматриваем несколько естественных расширений СМ, такие как модель с двумя дублетами Хиггса (2HDM), 2HDM и легкая скалярная модель, и модель зеркальной темной материи, которые позволяют увеличить Br (KS,L → invisible) до измеримого уровня. Мы кратко обсуждаем возможный поиск распадов KS,L → invisible и осцилляций KS,L в темном секторе в эксперименте NA64 в ЦЕРНе с чувствительностью к Br (KS,L → invisible) ≲ 10−7−10−5.
Данный обзор является введением в новейший раздел теории симметрий — теории квантовых групп.
Основы теории квантовых групп рассматриваются с точки зрения возможности их использования для деформаций симметрий в физических моделях. Подробно обсуждается R матричный подход к теории квантовых групп, который положен в основу квантования классических групп Ли, а также некоторых супергрупп Ли. Мы начинаем с изложения основ некоммутативных и некокоммутативных алгебр Хопфа. Большое внимание уделено R-матрицам Гекке и Бирман-Мураками-Венцля (BMW) и связанным с ними квантовым матричным алгебрам. Обсуждается некоммутативная дифференциальная геометрия на квантовых группах специальных типов. Представлены тригонометрические решения уравнений Янга-Бакстера, связанных с квантовыми группами GL_q(N), SO_q(N), Sp_q(2n) и супергруппами GL_q(N|M), Osp_q(N|2m), а также рациональные (янгианские) пределы этих решений. Также рассматриваются рациональные R-матрицы для исключительных алгебр Ли и эллиптические решения уравнения Янга Бакстера. Изложены основные понятия групповой алгебры группы кос и ее конечномерных факторов (таких как алгебры Гекке и BMW). Дан набросок теорий представлений алгебр Гекке и BMW, включая методы нахождения идемпотентов (квантовых проекторов Юнга) и их квантовых размерностей. Кратко обсуждаются приложения теории квантовых групп и уравнений Янга-Бакстера в различных областях теоретической физики.
Это модифицированная версия обзорной статьи, опубликованной в 2004 году в виде
препринта Института математики Макса Планка в Бонне.
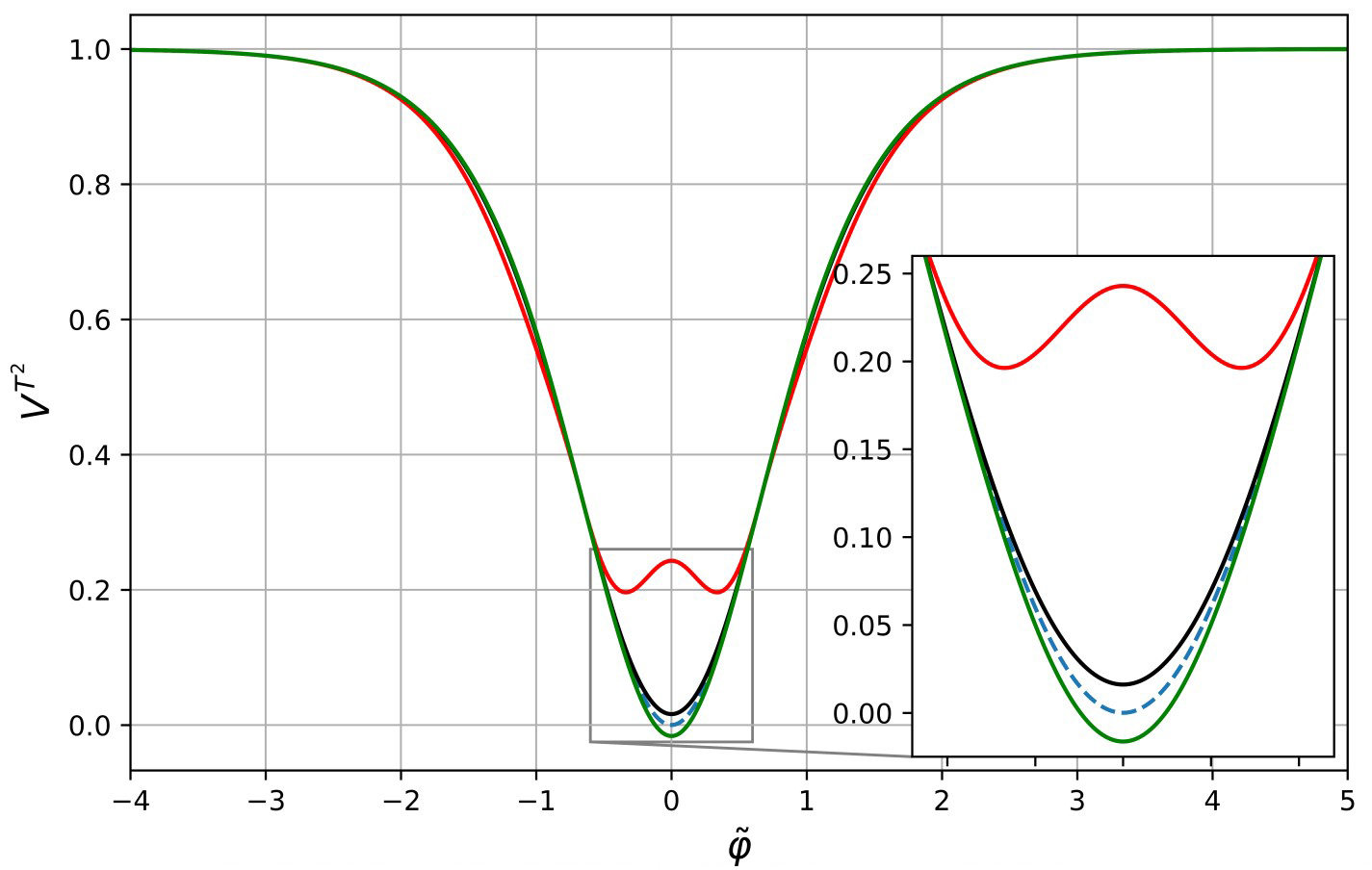
Используя аппарат обобщенной ренормализационной группы, мы вычисляем квантовые поправки к эффективному потенциалу в моделях α-аттракторов, описывающих инфляционную стадию расширения Вселенной. Продемонстрировано, что квантовые поправки приводят к изменению изначального минимума исходного классического потенциала, что можно интерпретировать как проявление космологической постоянной или темной энергии.
